Back in the NES era, one’s progress in games unlocked passwords that allowed you to continue the game from a certain level instead of the beginning. These codes have seen less use now that random access storage is more available.
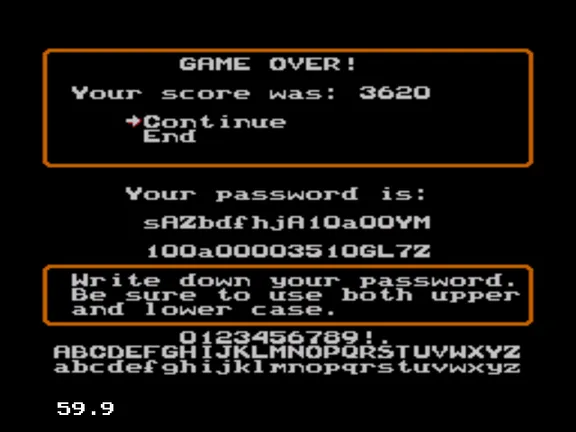
However, with the cloud and online features it is possible for players to create, exchange and share items in some game or application. However, concisely and uniquely identifying an item is difficult on gaming consoles because these do not have a concept of a clipboard or copy and paste. Otherwise universal UUIDs are cumbersome, and it is close to impossible to improve significantly from their hexadecimal representation, fe. a1229cf1-8422-464e-b612-693c9513932a.
The wide availability of smart phones makes sharing visual codes like QR codes or Aztec codes feasible. However, sharing these in text chats is not as easy as short text snippets.
Some web services like Bitly and Imgur encode their URLs using short text identifiers1. However, these URLs are case-sensitive, which is not ideal. Fortunately, many alternative and more human-friendly encoding schemes exist.
Design goals
The use case this design tries to solve is where a user has something in a game (or app) that other people can potentially also access either by searching or by knowing the ID of the item. It is also assumed that this game is on a television and the main input device is a gamepad. In other words, the user is left to either take a screenshot with their smartphone or copy a string that uniquely identifies the item. The user will then let their friends or the whole world know of their item using any medium, be it a text message or a YouTube video.
The four design goals are: short representation, unambigious characters, error detection and non-sequentiality. The three first ones are a bit at odds as both restricting the alphabet and adding error detection codes will increase the code length. For the use case, we prioritize that the code is sent and received right the first time so will sacrifice length so that the code is understood unambigiously.
In addition, this approach expects that the items are identified by reasonably small integers that can be sequential. In most cases digital things are identified in a database with an autoincrementing primary key.
The idea is to encode these numbers (primary keys, integers) as 8 character strings using the alphabet from Crockford’s Base322 but in the order of ZBase32. Crockford’s aim is to have an unambigious alphabet and ZBase32’s goal is to “make the more commonly occuring characters also be those that we think are easier to read, write, speak, and remember”.
In other words, we want the disambiguity and lack of vowels of Crockford but with the ordering rationale of ZBase323. Or as I call it, Zrockford.
Base32: ABCDEFGHIJKLMNOPQRSTUVWXYZ234567 ZBase32: ybndrfg8ejkmcpqxot1uwisza345h769 Crockford: 0123456789ABCDEFGHJKMNPQRSTVWXYZ Zrockford: YBNDRFG8EJKMCPQX0T1VW2SZA345H769
In addition to case-insensitivty, like in Crockford’s scheme, when decoding O and o are understood as 0 and I, i, L, l as 1.
The code will also use a check digit. Error detection is useful so that codes can be validated already on the client. To cover for most human transposition errors, Damm’s algorithm should do a great job4:
It […] will detect all occurrences of the two most frequently appearing types of transcription errors, namely altering one single digit, and transposing two adjacent digits (including the transposition of the trailing check digit and the preceding digit).
Using a 32 character alphabet (ie. each digit encodes log2(32) = 5 bits) and with 7 digits (in 8 character code XXXX-XXXY, Y is checksum leaving 7 digits for actual data) we can encode positive integers up to 2(8-1)×log2(32) = 27×5 - 1 = 34 359 738 368. To give some perspective to huge numbers, this gives roughly 4 items per everyone on Earth.
It is also desirable that two sequential codes would not encode to similar values: 1 would not encode to AAAA-AAAY and 2 to AAAA-AABY but for example ERDF-KMQC and 8EYE-RZ9J. There are at least two approaches to reversibly “hash” the value: modulo math or bit shifting5. Below I will use the first approach. Note that modulo math will require in some programming languages a library that can handle big numbers.
This approach is not optimal to get the shortest possible codes because we intentionally use more of the space to make codes different from each other.
The use of multiplicative inverses requires coming up with a magic number that is a co-prime with the integer after the maximum number that the scheme can handle. As luck would have it, it is very likely any random value is co-prime with our maximum number (ie. their greatest common divisor is 1). 5 777 025 351 is one such, but so are 857 485 741, 1 326 363, 58 758 775, …
This value will be the “step”, the value by which the input value is multiplied before moudulo. Setting this to 1 would make the codes sequential. The bigger the value, “more” the output is different from input. The only requirement is that the GCD is 1, which can be checked in code or with a calculator.
Code
Below is a Javascript implementation of functions that generate codes that have the properties above.
Note the code below depends on Javascript’s BigInt that at the time of writing is not supported on all browsers. It also uses ES6 modules (export), which are currently supported experimentally on Node6.
/**
* Use Crockford's Base32 idea with zBase32 alphabet order with Damm
* checksum digit
*/
const SYMBOLS = 'YBNDRFG8EJKMCPQX0T1VW2SZA345H769'; // zrockford32
const VALID_SYMBOLS = new RegExp('^[' + SYMBOLS + ']+$');
let DECODE_TABLE = {};
for (let i = 0; i < SYMBOLS.length; i++) {
DECODE_TABLE[SYMBOLS[i]] = i;
}
/**
* Magic numbers
*
* `MAX_NUMBER` is a large number that is larger than any number we will
* ever encode and the largest number we can represent with our code
* length and alphabet.
* Given code_length (excluding check digit) = 7 and base = 32 (length
* of alphabet), the number of codes that it can encode is given by
* 2^(code_length * log2(base)) = 34 359 738 368
*
* `COPRIME` is a number that has to be co-prime with `max_number`, it is
* the number the input value is multiplied with (ie. the step between
* successive integers). Any random integer is likely co-prime with
* `MAX_NUMBER`.
*
* `MULINV` is the multiplicative inverse of `COPRIME` and `MAX_NUMBER`.
*/
export const MAX_NUMBER = BigInt('34359738368');
const COPRIME = BigInt('5777025351');
const MULINV = BigInt('1393193079');
/**
* Encodes an integer using multiplicative inverses
*
* @param n - a BigInteger
* @returns a masked BigInteger
*
* @remarks
* See:
* - https://stackoverflow.com/questions/4273466/reversible-hash-function
* - https://ericlippert.com/2013/11/14/a-practical-use-of-multiplicative-inverses/
* - https://planetcalc.com/3311/
*/
function bitmask(n) {
let ret = (n * COPRIME) % MAX_NUMBER;
return ret;
}
/**
* Decodes an integer using multiplicative inverses
*
* @param h - a masked BigInteger
* @returns a BigInteger
*
*/
function unbitmask(h) {
let ret = (h * MULINV) % MAX_NUMBER;
return ret;
}
/**
* Calculates the Damm checksum for a Base32 encoded array of digits
*
* @param digits - an array of digits
* @returns checksum
*
* @remarks
* See:
* - https://stackoverflow.com/questions/23431621/extending-the-damm-algorithm-to-base-32
*/
function damm32(digits) {
let checksum = 0;
for (let i = 0; i < digits.length; i++) {
let digit = digits[i];
checksum ^= digit;
checksum <<= 1;
if (checksum >= 32) {
checksum ^= 37;
}
}
return checksum;
}
/**
* Converts an array of digits to string
* using alphabets YBNDRFG8EJKMCPQX0T1VW2SZA345H769
*
* @param digits an Array of base 32 digits
* @returns a string
*/
function toString(digits) {
let str = '';
for (let i = 0; i < digits.length; i++) {
str += SYMBOLS[digits[i]];
}
return str;
}
/**
* Normalizes a Base32 string:
* - Removes dashes (AA-BB -> AABB)
* - Converts string to uppercase (a -> A)
* - Converts ambigious characters (IiLlOo -> 111100)
*
* The resulting string contains only digits from
* YBNDRFG8EJKMCPQX0T1VW2SZA345H769
*
* @param str input string
* @returns a normalized string
*/
function normalize(str) {
let norm_str = str.toUpperCase().replace(/-/g, '').replace(/[IL]/g, '1').replace(/O/g, '0');
if (!VALID_SYMBOLS.test(norm_str)) {
throw "string '" + norm_str + "' contains invalid characters";
}
return norm_str;
}
/**
* Convert an array of digits to BigInt
*
* @param arr array of base 32 digits
* @returns a BigInt
*/
function fromArray(arr) {
let n = BigInt(0);
let pow = BigInt(1);
let base = BigInt(32);
for (let i = arr.length - 1; i >= 0; i--) {
n += BigInt(arr[i]) * pow;
pow = pow * base;
}
return n;
}
/**
* Convert a BigInteger to an array of Base32 integers
*
* @param n a BigInt
* @retunrns an array of integers in Base32
*/
function toArray(n) {
let ret = [];
let base = BigInt(32);
let left = n;
while (left >= base) {
let remainder = left % base;
left = left / base;
ret.push(Number(remainder));
}
ret.push(Number(left));
return ret.reverse();
}
/**
* Encodes a number to a code
*
* @param n a number
* @returns a string
*/
export function encode(n) {
if (n >= MAX_NUMBER) {
throw "Number is too large";
}
else if (n <= 0) {
throw "Number has to be a positive integer";
}
let digits = toArray(bitmask(BigInt(n)));
while (digits.length < 5) {
digits.unshift(0);
}
digits.push(damm32(digits));
let code = toString(digits);
return [code.slice(0, 4), code.slice(4, 8)].join("-");
}
/**
* Decodes a string to a number
*
* @param input an encoded string
* @returns a number
*/
export function decode(input) {
let str = normalize(input);
let digits = [];
for (let i = 0; i < str.length; i++) {
digits.push(DECODE_TABLE[str[i]]);
}
if (damm32(digits) != 0) {
throw "invalid check value '" + SYMBOLS[digits[digits.length - 1]] + "' for string '" + str + "'";
}
digits.pop();
let number = unbitmask(fromArray(digits));
return Number(number);
}
The above code should encode(123456) to DD7D-96YY. The full code can be found on GitHub.
Discussion
One possible optimization could be to use the rationale behind ZBase32 and try to order the alphabet so that the characters that are nearby on (virtual) keyboards are more common to ease input on gamepads and such.
Another improvement would be to make the scheme increase the size of the code dynamically. In most practical cases it is dangerous to set a too low maximum value7, but it would be nice if instead of preparing for the worst of 34 359 738 368 possible items with 8 digit codes, one could begin for example with 6 digit codes that would suffice for the first 2(6-1)×log2(32) = 33 554 432 items.
It is also possible to shorten the alphabet to Base168. In such case, continuing the inspiration from ZBase32 and Crockford’s Base32 would be to use the alphabet BNDRFGKMCPQXTWZH (Zrockford16). With 8 digits, this limits us to 268 435 456 codes and with 6 digits to just 1 048 576.
It might also be worthwhile to see if it’s possible to add also error recovery to the code so that a typo doesn’t invalidate the code. With the current design it is theoretically possible to use brute force and iterate over each digit and see if changing one of them makes the code “correct” and a corresponding item is available on the server or in the game.